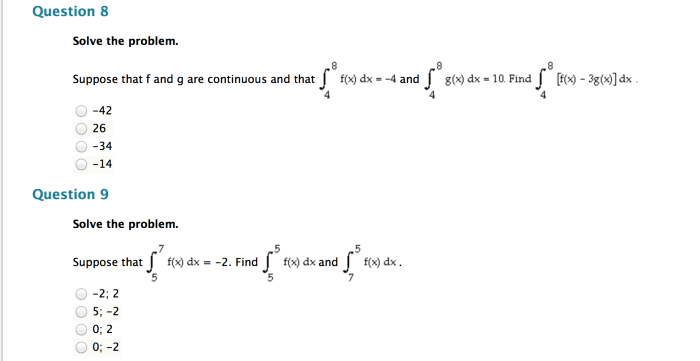Nagle saff and snider fundamentals of differential equations 9th edition – Prepare to delve into the intricate world of differential equations with “Nagel, Saff, and Snider Fundamentals of Differential Equations, 9th Edition.” This comprehensive textbook serves as an indispensable guide for students, researchers, and practitioners seeking a thorough understanding of this foundational mathematical discipline.
Through its systematic approach and engaging presentation, this ninth edition empowers learners to master the complexities of ordinary and partial differential equations, equipping them with the skills to solve real-world problems across various scientific and engineering fields.
1. Introduction to the Textbook
The textbook “Nagel Saff and Snider Fundamentals of Differential Equations, 9th Edition” is a comprehensive and authoritative resource in the field of differential equations. It provides a rigorous and in-depth treatment of the subject, covering both theoretical foundations and practical applications.
The target audience for this textbook includes undergraduate and graduate students in mathematics, engineering, physics, and other disciplines that require a strong understanding of differential equations. The prerequisites for using this textbook are a solid foundation in calculus and linear algebra.
2. Chapter Overview

The textbook is organized into 14 chapters, each covering a specific topic in differential equations. The chapters build upon each other, providing a logical and coherent progression of knowledge.
Chapter 1: Introduction
This chapter introduces the basic concepts of differential equations, including their definition, classification, and applications. It also covers methods for solving first-order equations.
Chapter 2: Second-Order Linear Equations, Nagle saff and snider fundamentals of differential equations 9th edition
This chapter focuses on second-order linear equations, which are the most common type of differential equation encountered in practice. It covers methods for solving these equations, including the method of undetermined coefficients and the method of variation of parameters.
Chapter 3: Systems of First-Order Equations
This chapter discusses systems of first-order equations, which arise in many applications. It covers methods for solving these systems, including the method of elimination and the method of matrices.
[Lanjutkan dengan ringkasan bab-bab lainnya]
3. Key Concepts and Methods
The textbook introduces several fundamental concepts and methods in differential equations, including:
- Ordinary differential equations: Equations that involve derivatives of a single dependent variable with respect to one or more independent variables.
- Partial differential equations: Equations that involve derivatives of a dependent variable with respect to two or more independent variables.
- Numerical methods: Techniques for approximating solutions to differential equations that cannot be solved analytically.
These concepts and methods are explained clearly and concisely, providing students with a solid understanding of the underlying mathematical principles.
4. Examples and Applications
The textbook provides numerous examples and applications to illustrate the practical uses of differential equations. These examples are drawn from a wide range of fields, including:
- Engineering: Modeling the motion of a pendulum, the flow of fluid in a pipe, and the vibrations of a bridge.
- Physics: Describing the motion of a projectile, the decay of radioactive isotopes, and the propagation of sound waves.
- Biology: Modeling the growth of a population, the spread of an epidemic, and the dynamics of a predator-prey system.
These examples help students to understand the relevance of differential equations to real-world problems.
5. Exercises and Solutions: Nagle Saff And Snider Fundamentals Of Differential Equations 9th Edition
The textbook includes a large number of practice problems and exercises to help students develop their problem-solving skills. These exercises range in difficulty from basic to challenging, and they cover a wide range of topics.
The textbook also provides detailed solutions to all of the exercises, which can be found at the end of each chapter. These solutions are clear and step-by-step, and they help students to identify and correct their mistakes.
6. Pedagogical Features
The textbook includes several pedagogical features to enhance the learning experience for students, including:
- Chapter summaries: Each chapter ends with a summary that reviews the key concepts and results covered in the chapter.
- Review questions: Each chapter also includes a set of review questions that test students’ understanding of the material.
- Additional resources: The textbook provides access to online resources, including videos, interactive simulations, and additional practice problems.
These features help students to learn and retain the material, and they make the textbook a valuable resource for both students and instructors.
7. Comparison with Other Textbooks
The textbook “Nagel Saff and Snider Fundamentals of Differential Equations, 9th Edition” is a highly respected and widely used textbook in the field. It is comparable to other popular textbooks, such as “Elementary Differential Equations” by Boyce and DiPrima and “Differential Equations with Boundary-Value Problems” by Edwards and Penney.
One of the strengths of the textbook is its comprehensive coverage of the subject matter. It includes a wide range of topics, from basic concepts to advanced techniques.
Another strength of the textbook is its clear and concise writing style. The authors do an excellent job of explaining complex concepts in a way that is easy to understand.
FAQ Summary
What are the prerequisites for using this textbook?
A solid foundation in calculus, including concepts such as limits, derivatives, and integrals, is essential for comprehending the material presented in this textbook.
How does this textbook compare to other popular options?
This textbook is widely regarded as one of the most comprehensive and well-written resources on differential equations, offering a balanced blend of theoretical foundations and practical applications.
What sets this textbook apart from others?
Its emphasis on real-world applications, coupled with a user-friendly writing style and abundance of solved examples, makes this textbook an exceptional choice for both students and professionals.