Embark on an enlightening journey with the AP Stats Chapter 6 Practice Test, where you will delve into the captivating world of data analysis and statistical inference. This comprehensive guide unlocks the secrets of data distributions, sampling distributions, hypothesis testing, and confidence intervals, empowering you to make informed decisions based on statistical evidence.
As you navigate through this practice test, you will encounter real-world examples that vividly demonstrate the practical applications of statistical methods. Prepare to be captivated by the power of data and the transformative impact it has on decision-making in various fields.
Exploring Data Distributions: Ap Stats Chapter 6 Practice Test
Understanding data distributions is paramount in AP Statistics Chapter 6. Data distributions provide insights into the shape, center, and spread of data, helping statisticians make informed inferences about populations.
There are various types of data distributions, including normal distributions, skewed distributions, and uniform distributions. Each distribution has unique characteristics, such as symmetry, kurtosis, and outliers.
Graphical Representations
Graphical representations, such as histograms, box plots, and scatterplots, are invaluable for analyzing data distributions. These graphs visually display the distribution of data, making it easier to identify patterns, trends, and potential outliers.
Sampling Distributions
Definition and Significance
Sampling distributions are probability distributions of sample statistics (e.g., sample mean or sample proportion) from all possible samples of a given size drawn from a population.
Sampling distributions are significant because they allow statisticians to make inferences about the population based on a sample. They provide insights into the variability of sample statistics and the likelihood of obtaining specific sample results.
Sampling Error and the Central Limit Theorem
Sampling error refers to the difference between the true population parameter and the sample statistic. The Central Limit Theorem states that as the sample size increases, the sampling distribution of the sample mean approaches a normal distribution, regardless of the shape of the population distribution.
Hypothesis Testing
Steps Involved
Hypothesis testing involves the following steps:
- State the null and alternative hypotheses.
- Set the significance level (alpha).
- Calculate the test statistic.
- Determine the p-value.
- Make a decision (reject or fail to reject the null hypothesis).
Null and Alternative Hypotheses
The null hypothesis (H0) represents the claim that there is no significant difference or relationship between variables. The alternative hypothesis (Ha) represents the claim that there is a significant difference or relationship.
P-Values and Statistical Significance
The p-value is the probability of obtaining a test statistic as extreme as or more extreme than the observed test statistic, assuming the null hypothesis is true. A small p-value (typically less than 0.05) indicates statistical significance, suggesting that the observed result is unlikely to occur by chance alone.
Confidence Intervals
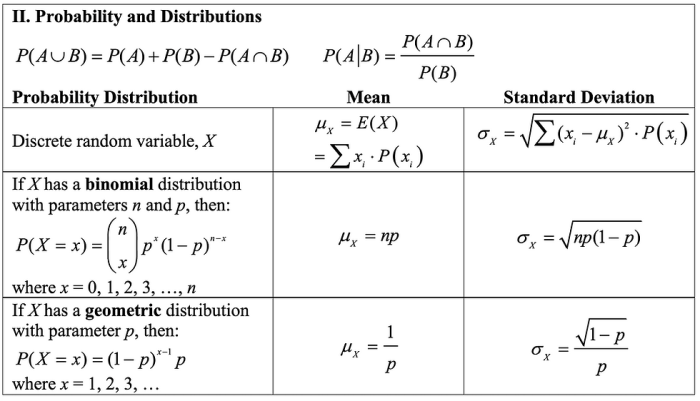
Definition and Purpose
Confidence intervals are ranges of values that are likely to contain the true population parameter with a specified level of confidence.
Confidence intervals are constructed using sample data and a margin of error. The margin of error is determined by the sample size, the variability of the data, and the desired level of confidence.
Methods for Construction, Ap stats chapter 6 practice test
There are various methods for constructing confidence intervals, including the t-distribution for sample means and the normal distribution for sample proportions.
Interpretation and Application
Confidence intervals provide a range of plausible values for the population parameter. They are useful for making inferences about the population and assessing the precision of the sample estimate.
Applications in Real-World Scenarios
Examples of Application
AP Statistics Chapter 6 concepts are widely applied in various fields, including:
- Healthcare: Analyzing patient data to identify risk factors and develop treatments.
- Business: Market research, customer satisfaction surveys, and quality control.
- Education: Assessing student performance and evaluating teaching methods.
- Social sciences: Conducting surveys, analyzing social trends, and making policy decisions.
Practical Significance
Data analysis and statistical inference are essential for making informed decisions in various real-world scenarios. They provide insights into data, help identify patterns and trends, and allow for evidence-based decision-making.
General Inquiries
What is the significance of data distributions in AP Statistics Chapter 6?
Understanding data distributions is crucial as they provide insights into the patterns and characteristics of data. Different types of distributions, such as normal, skewed, and bimodal, have unique properties that influence statistical inferences and decision-making.
How does the Central Limit Theorem impact sampling distributions?
The Central Limit Theorem states that as sample size increases, the sampling distribution of sample means approaches a normal distribution, regardless of the shape of the population distribution. This property is essential for making inferences about population parameters based on sample data.
What is the role of p-values in hypothesis testing?
P-values quantify the strength of evidence against the null hypothesis. A small p-value indicates that the observed data is unlikely to have occurred under the assumption of the null hypothesis, providing support for the alternative hypothesis.